[오늘의 문제]
https://www.acmicpc.net/problem/11052
[오늘의 학습 키워드]
- DP, 구현
1. 문제설명

문제가 길어서 복잡해 보이지만 쉽게 요약하면
구매하려는 카드의 개수 N이 주어질 때 카드 가격별로 가장 비싸게 카드를 구매하는 방법을 작성하는 프로그램을 구현하는 문제 입니다.
1 5 6 7은 각 카드별 금액으로
카드 1장 구매하는데는 1원
카드 2장 구매하는데는 5원
카드 3장 구매하는데는 6원
카드 4장 구매하는데는 7원 입니다.
각각의 금액별로 패키징 된 카드들이고 여기서 가장 카드를 비싸게 사는 방법은 2장짜리 카드를 2번 사는 경우의 수 입니다.
[제한사항]
- 시간 제한 1초
- 메모리 제한 256MB
- 1 ≤ N ≤ 1,000
- 1 ≤ Pi ≤ 10,000
2. 접근방식
이 문제는 N장의 카드를 구매하기 위해서 가장 비싸게 사는 경우의 수를 찾아가는 과정을 생각하면 됩니다.
카드 1장을 구매하는데는 1장짜리 패키지 밖에 구매하지 못하니 1원이 되겠죠
카드 2장을 구매하는데는 1장짜리 패키지 2개와 2장짜리 패키지 1개가 존재하는데 이때 더 비싼 것은 2장 짜리 패키지 이죠
카드 3장을 구매하는데는 1장짜리 패키지 3개, 2장짜리 패키지 1개 1장짜리 패키지 1개, 3장짜리 패키지 1개가 존재하고 이때 가장 큰 값을 구하면 되죠
이런식으로 N개의 카드를 구매하는 경우의 수를 채워주는데 DP테이블을 이용해서 매 순간 비싼 카드를 구매하는 방법으로 채워주면 됩니다.
그럼 점화식을 세워야 하는데 이런식으로 접근해 볼 수 있죠
DP = [0] x (N + 1) 로 생성합니다.
DP 테이블에 카드의 구매 장수와 비용을 계산하기 위해서는 중첩 반복문을 사용해 i, j로 풀어주어야 합니다.
첫 반복문 i에서는 카드의 구매 장수를 의미하고
두번째 반복문 j에서는 현재 구매하려는 카드장수 입니다.
즉 첫번째 반복문에서는 전체 N장의 카드중 i장의 카드를 구매할 때 카드의 비용을 고정하여 계산하기 위해서 i가 필요하고
j는 모든 경우의 수를 계산해 주는 것입니다.
j는 현재 구매하려는 카드의 개수를 의미하죠 이렇게 생각해보죠
DP 테이블은 매 순간 가장 비싼 카드의 비용으로 구매하고 있었습니다.
그럼 DP[j] 는 j장의 카드를 구매하는 가장 비싼 경우의 수가 들어가야 겠죠
처음 카드를 구매하는 경우 DP[1] 부터 DP[N] 까지 우선적으로 DP 테이블이 채워지게 됩니다.
여기서 DP[j] 번째 카드를 가장 비싸게 사기 위해서는 현재 채워진 DP[j] 와 새롭게 채워질 DP[j] 중 더 비싼 경우의 수를 비교해 주어야 겠죠
새롭게 채워질 DP[j]는 구매하려는 카드에 현재 기준이 되는 i의 카드팩의 금액을 이용해 주어야 겠죠
쉽게말해 j번째 카드를 구매할 때 j에서 i번째 카드를 제외하면 i번째 카드가 추가되는 가장 비싼 경우의 수를 구할 수 있죠
DP 테이블은 매번 가장 비싼 경우의 수만 구해오기 때문에요
기준이 되는 i번째 카드를 제외한 가장 비싼 경우의 수는 DP[j - i] 를 통해 가장 비싼 경우의 수를 찾을 수 있는데 여기에 i번째 카드의 비용을 더해주어야 겠죠
그럼 DP 테이블의 점화식은 다음과 같이 구성됩니다.
DP[j] = max(DP[j], DP[j - i + cards[i])
cards에 각 카드별 구매 비용이 저장되어 있을때 DP[j] 번째 카드 구매 비용중 가장 비싸게 사는 경우를 찾기 위해서는
기존에 정의된 DP[j] 와 j에서 기준값 i를 빼주고 새롭게 카드의 비용 i를 더해주었을때 2경우를 비교해주면 되겠죠
여기서 주의할 점은 j - i 가 비교하려는 카드의 인덱스 범위 안쪽이어야 합니다.
따라서 j - i >= 0 인 경우에만 가장 비싸게 사려는 카드의 경우를 구할 수 있습니다.
이를 그대로 코드로 구현해 보았습니다.
3. 코드
import sys
input = sys.stdin.readline
# 입력
N = int(input())
cards = [0] + list(map(int, input().split())) # 카드의 구매 비용, index 맞추기 위해 0 삽입
DP = [0] * (N + 1) # 최대값 구해야 하니 DP를 0으로 초기화 하며 생성
# 점화식 i는 기준값
for i in range(1, N + 1):
# j는 비교값
for j in range(1, N + 1):
# index 범위 맞추기
if j - i >= 0:
DP[j] = max(DP[j], DP[j - i] + cards[i])
print(DP[N])[코드설명]
앞선 접근방식을 그대로 코드로 구현한 것입니다.
현재값 j에서 기준값 i를 빼주면 i가 추가할 때 가장 비싸게 추가하는 경우의 수를 찾을 수 있고 그 값이 기존의 값과 비교했을때 더 큰 경우 바뀌게 되겠죠
그러나 index 범위를 생각해서 j - i가 0보다 크거나 같은 경우에만 실시해 줍니다.
간단하게 동작을 살펴보죠

cards에 카드의 비용을 저장하고 index를 맞추기 위해 0을 삽입해 주었습니다.
그리고 최대값을 구하기 위해 DP는 0으로 생성해 주었죠
이제 기준값 1 즉, 1장의 카드로 구매하는 경우를 살펴보죠
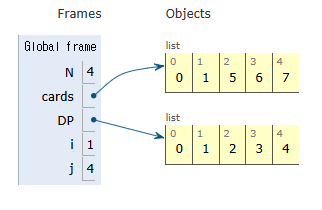
1장의 카드를 구매할 때 j는 매번 이전에 구매한 카드 비용에 새롭게 1장을 추가하는 경우를 비교하게 됩니다.
DP 테이블은 0으로 초기화 되어 있었으니 최초 실행을 통해 1장의 카드비용으로 1장부터 N장까지 구매하는 경우 가장 비싸게 사는 경우를 구해주었죠
이제 2장의 카드 패키지로 카드를 구매하는 경우를 보죠

여기서 i는 기준값이 2입니다. 즉, 2장의 패키지로 카드를 N장 까지사는 경우죠
그러나 j는 1부터 모든 경우를 구해야 합니다 j-i 는 현재 -1이니 조건을 충족하지 않습니다.
2장의 카드 패키지로 1장을 살수는 없기 때문이죠

2개의 패키지로 2장을 사는경우 기존의 비용 2와 새롭게 비교할 비용 0에 5를 더한 5중 더 큰 값 5가 채워졌습니다.
동일하게 4번째 카드를 구매하는 경우를 살펴보면
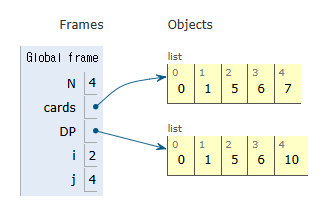
기존 2장의 카드 패키지로 2개의 카드를 구매하는 경우 5의 비용으로 카드를 구매했습니다. 4장을 사기 위해서는 현재 구매하려는 카드 장수에서 기준값을 제외해주면 DP[2]가 되고 이때 가장 비싸게 산 경우가 저장되어 있죠
여기에 새롭게 카드 2장을 추가하는 비용을 더해주는 겁니다.
이럼 10이 되죠
동일하게 3장을 사는 경우도 채워주었습니다.
모든 동작을 완료하여도 10보다 더 비싸게 사는 경우가 없기 때문에 10이 출력되는 것입니다.
4. 결과

[회고]
이번 문제는 저번 시간에 풀었던 문제와 비슷했습니다.
저번에 동전2 문제를 풀면서 비슷하게 문제를 한번 풀어보았죠
이번에도 처음에는 이와 비슷하게 점화식을 세워서 문제를 풀려고 했는데 값이 제대로 구해지지 않더라구요
그때 세웠던 점화식이 카드의 비용을 이용해서 카드의 구매장수를 제한하고 있었고 이러니 index도 맞지 않고
카드 구매 장수도 맞지 않아서 틀렸었습니다.
따라서 비용이 아닌 index로 접근했고 1장의 패키지로 구매하는 경우 DP에 누적합을 이용해 최고값을 작성해 나갈 수 있었고 문제를 해결할 수 있었습니다.
계속해서 DP 문제를 풀어보며 실력을 키우고 있는데 여전히 난이도가 조금만 높아지면 어려운것 같습니다. 아직 응용이 부족해서
그런것 같습니다. 여러 문제를 풀며 다양하게 DP를 세우며 정의해보고 많은 문제를 풀어보아야 할 것 같습니다.
'알고리즘' 카테고리의 다른 글
| [백준] 2293 동전 1 -골드 4 (0) | 2025.05.25 |
|---|---|
| [백준] 1699 제곱수의 합 - 실버 2 (0) | 2025.05.24 |
| [백준] 2294 동전 2 - 골드 5 (2) | 2025.05.21 |
| [백준] 1912 연속합 - 실버 2 (0) | 2025.05.20 |
| [백준] 11053 가장 긴 증가하는 부분 수열 - 실버 3 (0) | 2025.05.19 |