[오늘의 문제]
https://www.acmicpc.net/problem/2579
[오늘의 학습 키워드]
- 다이나믹 프로그래밍, 점화식
1. 문제설명

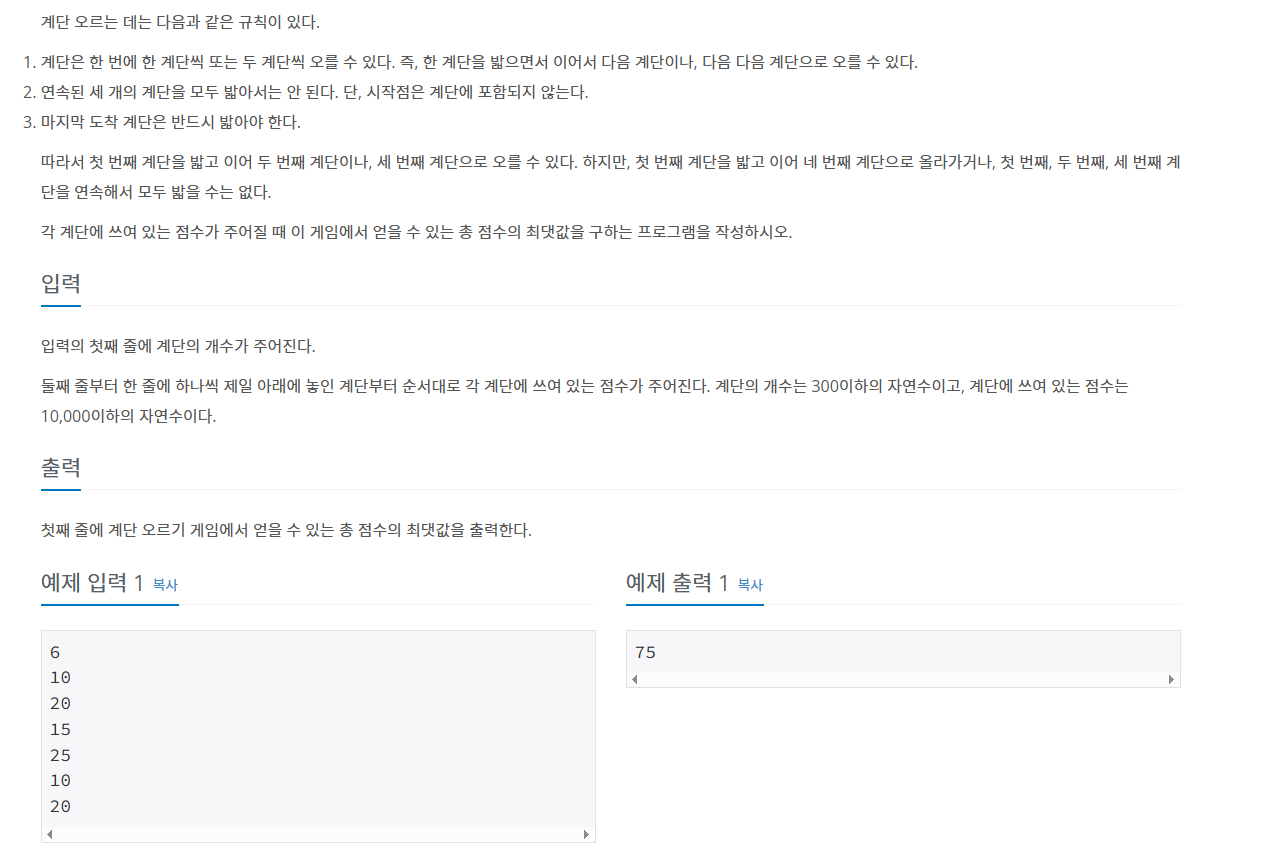
오르려는 계단이 N개 주어질 때 계단을 오를 때마다 계단에 적힌 점수를 얻습니다.
계단은 연속해서 3칸 이상 오를 수 없습니다.
즉 4번째 계단을 가기 위해서는 1, 2, 4 로 가거나 1, 3, 4 로 올라가야 합니다.
계단을 올라 N번째 계단에 도착할 때 얻을 수 있는 최대값을 구하는 프로그램을 작성해야 합니다.
[제한사항]
- 시간 제한 1초
- 메모리 제한 128MB
- 계단은 300개 이하
- 점수는 10,000 이하
2. 접근 방식
이 문제는 N번째 계단이 어떻게 올라왔을 까를 고려하는 점화식을 세우는 문제입니다.
처음부터 차근차근 생각해 보겠습니다.
1. 계단을 1칸 오를 때 입니다.
- 1칸을 오르기 위해서는 시작점에서 1칸 올라가야 합니다.
2. 계단을 2칸 오를 때 입니다.
- 2칸을 오르기 위해서는 시작점에서 1칸, 1칸에서 2칸으로 올라야 합니다.
3. 계단을 3칸 오를 때 입니다.
- 3칸을 오르기 위해서는 시작점에서 1칸, 1칸에서 3칸으로 오르는 방법이 있습니다.
- 또 시작점에서 2칸, 2칸에서 3칸으로 오르는 2가지 방법이 존재합니다.
4. 계단을 4칸 오를 때 입니다.
- 1 -> 2 -> 4
- 1 -> 3 -> 4
- 2 -> 4
3가지 경우의 수가 존재합니다.
이때 1 -> 2 는 계단을 2칸 오르는 방법과 동일합니다. 또 1 -> 3-> 4 에서 1은 계단을 1칸 올라가는 방법과 동일합니다.
여기서 점화식을 세울 수 있습니다.
계단을 오르는 방법을 dp 배열에 작성할 때 dp[i] 번째 계단을 오르기 위해서는 dp[i - 2] 번째 계단에서 i번째 계단으로 올라가는 방법 과
dp[i - 3] 에서 i-1번째 계단과 i번째 계단을 밟고 올라오는 방법 2가지가 존재하고 그 중 더 큰 점수를 얻는 방법을 고르면 됩니다.
3. 코드
import sys
input = sys.stdin.readline
N = int(input())
stairs = [0] * 301
for i in range(1, N+1):
stairs[i] = int(input())
dp = [0] * 301
dp[1] = stairs[1]
dp[2] = stairs[1] + stairs[2]
dp[3] = max(stairs[1] + stairs[3], stairs[2] + stairs[3])
# dp[4] = max(dp[2] + stairs[4], dp[1] + stairs[2] + stairs[3])
# -> 점화식으로 변경해보자
# dp[i] = max(dp[i-2] + stairs[i], dp[i-3] + stairs[i-1] + stairs[i])
for i in range(4, N + 1):
# dp[3] 생각해보자 i가 2이고 i-1 이 1인 경우
dp[i] = max(stairs[i-1] + stairs[i] + dp[i - 3], stairs[i] + dp[i - 2])
print(dp[N])[코드설명]
우선 계단의 정보를 저장하기 위해서 계단 배열 stairs를 생성해 주었습니다.
계단은 총 300개 이하라고 했으니 1번 계단부터 300번 계단까지 순서를 맞추기 위해 301 까지 생성해 주었고 1, N + 1 까지 계단의 정보를 입력받아 줍니다.
계단의 정보를 토대로 dp배열을 작성할건데 dp[1]번은 1 dp[2]는 2 dp[3] 은 1, 3 또느 2, 3 중 더 큰 값을 가집니다.
여기서 dp[4]는 앞서 세운 점화식을 토대로 세워보면
dp[4] = dp[2] 번에서 계단 stairs[4]를 밟고 올라오는 방법
dp[4] = dp[1] 번에서 계단 stairs[3] 과 stairs[4]를 밟고 올라오는 방법이 존재합니다.
이 중 더 큰값을 dp[4]에 저장하면 되겠죠
이렇게 세운 점화식을 i를 이용해 변경하고 반복문을 이용해 dp 배열을 채워줍니다.
4. 결과

[회고]
DP 문제는 점화식을 어떻게 잘 세우냐에 따라서 문제를 쉽게 해결하거나 해결하지 못하거나 입니다.
즉, 점화식을 잘 세워야 하는데 이번 문제는 점화식을 찾기 조금 헷갈렸습니다.
이번 문제의 점화식은 3번 조건을 가장 많이 타는데 연속해서 계단을 3개이상 올라갈 수 없기에 처음에는 백트래킹으로 문제를 해결하려 했으나 틀렸었습니다.
원래도 DP 문제를 잘 못하는데 처음에는 계단을 무작정 아래에서 위로 올라가는 방식으로 점화식을 세워 문제를 해결하려 했어서 틀렸습니다.
틀린 후 현재 계단을 기준으로 올라오는 경우의 수를 구해주었고 제대로된 점화식을 세울 수 있었습니다.
DP 문제의 경우 점화식을 세우기 위해서 조건을 생각할 때 1번 부터 약 4번 5번 까지는 손으로 조건을 그려본 후 그 사이에서 점화식을 찾는게 중요합니다.
이번 문제역시 4번 계단까지 올라가는 방법을 일일이 생각해보며 조건을 찾아보았고 5번 계단을 넘어가는 시점을 기준으로 점화식을 찾을 수 있었습니다.
그에 따라 4번 계단역시 점화식을 초기화 할 수 있었고 세운 점화식을 토대로 DP 배열을 초기화하고 stairs 배열을 건드리며 DP 배열을 채울 수 있었습니다.
이 문제를 해결하기 전 비슷한 DP 문제인 1, 2, 3 더하기 문제를 풀어보았습니다.
https://www.acmicpc.net/problem/9095
이 문제 역시 DP 문제로 점화식만 잘 세운다면 해결이 가능하였고 조건을 잘 찾아 N번까지 수를 더해주면 문제를 해결할 수 있습니다.
해당 문제 해결의 열쇠는 N번 수를 1, 2, 3 으로 더하는 갯수에 있습니다.
'알고리즘' 카테고리의 다른 글
| [백준] 1756 피자 굽기 - 골드 5 (0) | 2025.04.14 |
|---|---|
| [백준] 18405 경쟁적 전염 - 골드5 (1) | 2025.04.13 |
| [백준] 2580 스도쿠 - 골드 4 (0) | 2025.04.11 |
| [백준] 1987 알파벳 - 골드 4 (0) | 2025.04.10 |
| [백준] 2206 - 벽 부수고 이동하기 - 골드 3 (0) | 2025.04.09 |