[백준] 2011 암호코드 - 골드 5
[오늘의 문제]
https://www.acmicpc.net/problem/2011
[오늘의 학습 키워드]
- DP
- 구현
1. 문제설명

A를 1, B를 2, Z를 26 이라고 암호화 하였습니다.
첫째 줄에 5000자리 이하의 암호가 주어질 경우 이 암호로 만들 수 있는 모든 경우의 수를
찾아 출력하는 프로그램을 작성하는 문제 입니다.
[제한사항]
- 시간 제한 2초
- 메모리 제한 128MB
- 첫째 줄에 5000자리 이하의 암호가 주어진다.
- 정답이 매우 크니 1000000으로 나눈 나머지를 출력
2. 접근방식
굉장히 어려운 문제 였습니다.
문제를 풀기 위해서는 각 숫자를 자릿수의 개념으로 접근해 보아야 합니다.
예시로 25114 를 복호화 하는 과정을 거쳐 경우의 수를 찾아 보겠습니다.
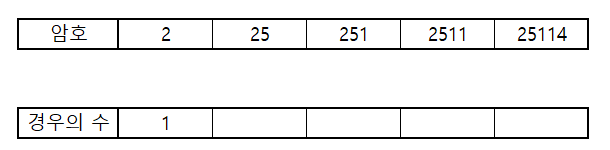
우선 25114 중 한자리만 들어온 경우를 살펴보죠
1자리만 들어온 경우 어떤 수든간에 무조건 1개의 경우의 수가 나옵니다.
A가 1이고 Z가 26이니 모든 숫자는 알파벳으로 치환이 가능한데 1자리만 들어온 경우 경우의 수는 1부터 9까지만 존재하는 알파벳이기 때문에 무조건 1개의 경우의 수가 나오게 되죠

두자리가 들어온 경우 경우의 수는 2개가 나옵니다.
1자리 2, 5 로 각각 1개의 경우의 수와
2자리 25 로 1개의 경우의 수가 존재하여 총 2개의 경우의 수가 존재하죠
이때 한가지 검증을 실시해야 합니다.
들어온 숫자가 10보다 커야하고 26보다는 작아야 알파벳으로 치환이 가능하기때문에
현재 탐색중이 글자를 기준으로 이전 글자의 숫자에 x 10을 해주고 현재 글자를 상징하는 숫자를 더했을 때
10보다 크고 26보다 작아야 하겠죠
이걸 일반화 시킨다면 아래와 같습니다.
if 10 <= words[i - 1] x 10 + words[i] <= 26
이렇게 검증해야 하죠
이때의 경우의 수는 2자리가 존재하게 됩니다.
3자리가 들어온 경우를 살펴보죠

3자리가 들어온 경우 경우의 수는 현재 2개가 존재합니다.
2 / 5 / 1
25
2개가 존재하죠
1의 자리의 경우 0보다 크기만 하면 되기 때문에 현재 경우의 수는 이전 1자리만 찾은 경우의 수와 동일할 겁니다.
여기에 새로운 숫자가 더해진다 한들 크게 달라질건 없죠
동일하게 25 / 51 을 검증을 거쳐야 하는데
25의 경우 10 이상 26이하의 조건에 만족하니 1개의 경우의 수로 인정 받습니다.
51의 경우 조건을 만족하지 않으니 1개의 경우의 수로 인정받지 못합니다.
1개의 경우의 수는 현재 자리를 기준으로 2 이전의 값이죠?
이 값을 더해주면 될 것 같습니다.
동일하게 2511을 검증해 보겠습니다.

우리는 주어진 자릿수에 대해 일반화를 거쳐 경우의 수를 찾아주어야 합니다.
2511의 경우 기존 251에서 찾은 경우의 수에 새로운 검증이 필요합니다.
새롭게 들어온 1이 0보다 큰지에 대한 검증과
이전의 수에 x 10을 하고 1을 더했을때 10보다 크고 26보다 작은지에 대한 검증이 필요하죠
새롭게 들어온 1의 경우 0보다 크기 때문에 이전의 경우의 수에 1을 추가한 모양이 됩니다.
11의 경우도 10보다 크고 26보다 작기 때문에 조건을 만족하죠
즉 새롭게 들어온 숫자가 0보다 크고 두 수를 이용한 숫자가 10보다 크고 26보다 작다면 경우의 수가 2개 늘어나는 것이죠
이조건을 일반화 하기 위해 DP를 이용해야 합니다.
기존에 DP값을 이용해 경우의 수를 누적해야 하죠 새롭게 들어온 수가 1보다 크다면 경우의 수를 1 늘려야 하고, 10보다 크고 26보다 작다면 또 1을 늘려야 하죠
그렇다면 더욱 쉽게 경우의 수를 관리하려면 0보다 크기만 하다면 기존의 경우의 수를 그대로 가져오고
2번째 조건을 만족한다면 경우의 수를 2개 늘려주면 되겠죠
이게 가능한 이유를 찾으려면 2555를 생각해 보면 됩니다.
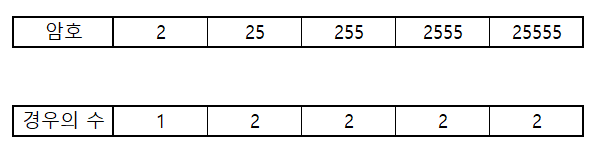
25555의 경우 경우의 수는 무조건 2개 밖에 되지 않습니다.
왜냐하면 2의 경우 경우의 수 1개가 존재하는데, 25가 가능하니 2개가 되는 것입니다.
그러나 그 뒤부터 55,55,55, 가 반복되는데 이는 모두 알파벳으로 치환이 불가능한 숫자입니다.
즉 이때의 암호를 복호화 한다면 나올 수 있는 알파벳은 BEEEE 혹은 YEEE 두개 뿐이기 때문입니다.
이 경우를 생각한다면 2511의 경우 나올 수 있는 알파벳은
BEAA, BEK, YAA, YK 로 4개가 존재하죠
따라서 일반화 하려면 다음과 같은 점화식이 생성됩니다.
# 일의 자리 경우의 수는 그대로 가져오기
if words[i] >= 0:
DP[i] = DP[i] + DP[i - 1]
# 십의 자리 경우의 수는 조건을 만족한다면 2개씩 늘어나야 한다.
if 10 <= words[i - 1] * 10 + words[i] <= 26
DP[i] = DP[i] + DP[i - 2]
여기서 DP[i - 2] 가 가능한 이유는 주어진 숫자가 2자리 일때 경우의 수가 조건만 만족한다면 2가 되기 때문에 2개의 경우의 수가 존재하고
기존의 경우의 수에 2개씩 늘려주면 되기 때문에 이러한 점화식이 생성되는 것입니다.
이를 바탕으로 코드를 작성해 보았습니다.
3. 코드
import sys
input = sys.stdin.readline
# 입력
words = list(map(int, input().strip())) # 공백 X
N = len(words)
# DP 테이블 생성 및 초기화
DP = [0] * (N + 1)
DP[0] = 1 # 0의 경우 점화식 계산을 맞추기 위해 1로 초기화
DP[1] = 1 # 1자리는 무조건 1개의 경우의 수 존재
# 모두 무시하고 words가 0이 주어진다면 경우의 수 0개
if words[0] == 0:
print(0)
# 경우의 수가 존재하는 자릿수가 주어진다면 점화식을 토대로 계산해주기
else:
# words 와 DP 테이블을 선택해야 하므로 i와 j를 이용해 index 맞추기
for j in range(1, N):
i = j + 1
# 일의 자리 경우 이전 경우의 수 그대로 더해주기
if words[j] > 0:
DP[i] = DP[i] + DP[i - 1]
# 십의 자리 경우 기존의 경우의 수에 2개를 늘려줘야 한다.
if 10 <= words[j - 1] * 10 + words[j] <= 26:
DP[i] = DP[i] + DP[i - 2]
print(DP[N] % 1000000)[코드설명]
우선 입력이 주어질 때, 공백이 없이 주어지므로 이를 입력받기 위해 strip()을 이용해 주었습니다.
DP 테이블을 생성하고 초기화 하기 위해서는 입력받은 words의 길이가 필요하니 N으로 설정하고 이를 토대로 DP 테이블을 생성
하고 초기화 해주었습니다.
초기화 할때 DP 테이블의 점화식 계산을 위해서 0을 1로 초기화 해주었습니다.
N이 1, 즉 1자리가 주어진다면 무조건 1개의 경우의 수가 존재하기 때문에 DP[1] 역시 1로 초기화 해주었죠
그 다음 입력으로 주어지는 words의 자릿수에 따라 출력을 달리 해주었습니다.
words가 0이 주어진다면 경우의 수가 0개로 0이 출력되어야 하는데 점화식 계산을 위해 DP[0]을 1로 초기화 하였기때문에
이 경우를 구분해 주어야 합니다.
따라서 0이 주어진다면 0을 출력해주었고 그게 아니라면 점화식을 토대로 계산을 실시해 주어야 하죠
점화식의 경우 찾아놓은 2가지 점화식을 토대로 계산을 실시해 주어야 하는데
DP 테이블은 2번부터 작성되어야 하는데 words는 1번부터 접근이 되어야 제대로된 계산 수행이 가능합니다.
따라서 2개의 인덱스를 맞추기 위해 j를 1부터 N까지 선언하고 i를 j + 1로 선언하여 인덱스를 맞춰 주었습니다.
그 후 찾은 점화식을 토대로 계산을 실시해주고 결과를 출력해 주었습니다.
4. 결과

[회고]
이번 문제는 좀 어려웠습니다.
처음에 35%에서 틀려서 이유를 찾던중 문제에서 5000자리 이하의 암호가 주어진다 하였고 1 이상이란 말이 없어서 0의 경우를 구분해 주었습니다.
점화식을 생각보다 빨리 찾았는데 0의 경우를 구분하고 인덱스를 맞추는 과정이 조금 오래 걸렸습니다.
그러다 찾은 방식이 j와 i를 이용해 인덱스를 구분하는 방법 이었고, j는 1부터 i는 2부터 탐색을 시작하여 제대로된 탐색을 수행할 수 있었습니다.
또한 점화식을 찾기 위해서 자릿수 계산과 경우의 수 계산은 제대로 수행하였는데 일반화 하는 과정이 오래 걸렸습니다.
DP 테이블을 이용하여 기존의 값을 토대로 누적 경우의 수를 생성해 주어야 하는데 조건에 맞는 경우만 2개의 경우의 수를 늘려주어야 했습니다.
그러면 기존의 경우의 수를 그대로 가져왔을때, 10의 자리 경우의 수가 맞다면 2를 늘려주어야 하는데 이 마저도 조건이 맞는 경우가 있고 틀리는 경우가 있어서 DP를 이용해 값을 구분해 주어야 했습니다.
그냥 2를 더해버리면 제대로된 점화식이 생성되지 않았기에 기존의 값에 이전값을 토대로 값을 늘려가야 했고 i - 2 를 찾은 것이죠
어렵게 어렵게 풀다보니 문제를 풀면서 인덱스 위치와 조건이 조금 헷갈렸는데
블로그를 작성하며 남에게 설명해주려 작성하다 보니 오히려 더 쉽게 이해가 되었습니다.
다음에도 비슷한 문제를 풀면서 DP 실력을 계속 키워보겠습니다.